Lớp 6
Bài 1: Tập Hợp - Khái niệm và thuật ngữ
1. Khái niệm cơ bản:
- Tập hợp: Một khái niệm toán học dùng để mô tả một nhóm các đối tượng hoặc số liệu.
- Phần tử: Các đối tượng cá biệt trong một tập hợp.
- Tập rỗng: Một tập hợp đặc biệt không chứa phần tử nào.
2. Kiến thức và kỹ năng:
- Nhận biết tập hợp và phần tử của nó: Học sinh sẽ học cách phân biệt và nhận dạng các tập hợp cũng như các phần tử thuộc tập hợp đó.
- Mô tả một tập hợp: Cách diễn đạt và mô tả các tập hợp sử dụng ngôn ngữ và ký hiệu toán học.
- Sử dụng ký hiệu và cách diễn đạt toán học thông qua tập hợp: Áp dụng các ký hiệu toán học để biểu diễn và giải thích về các tập hợp.
3. Cách chơi và tính điểm:
- Các số sẽ xuất hiện ngẫu nhiên ở trong hoặc ở ngoài hình tròn, các em chọn ký hiệu ∈ hoặc ∉ thích hợp cho ô vuông?
- Trong quá trình luyện tập, mỗi lần xuất hiện 4 câu hỏi (a, b, c, d), đúng một câu được cộng 1 điểm, sai một câu bị trừ 1 điểm. Các em có thể luyện tập không giới hạn số lần để nâng cao kỹ năng của mình.
4. Lưu ý:
- Đừng quên đăng nhập để hệ thống có thể ghi nhận điểm số của bạn, giúp theo dõi tiến trình học tập và cải thiện kết quả.
Bài học này sẽ giúp các em xây dựng nền tảng vững chắc trong việc hiểu và sử dụng các khái niệm về tập hợp trong toán học, một kỹ năng cơ bản và quan trọng trong các chủ đề toán học tiếp theo. Chúc các em học tập hiệu quả và đạt được nhiều thành công!
Khái niệm và thuật ngữ
- Hệ thập phân
- Chữ số Ả Rập
- Số La Mã, chữ số la Mã
KIến thức và kỷ năng
- Nhận biết giá trị các chữ số của một số tự nhiên trong hệ thập phân
- Biểu diễn các số tự nhiên thành tổng giá trị các chữ số của nó
- Đọc viết Số La Mã từ 1 đến 30

Bài học: Cách viết số La Mã (Toán lớp 6)
Mục tiêu:
- Hiểu và nắm vững quy tắc viết số La Mã.
- Biết cách đọc và viết các số La Mã cơ bản.
- Áp dụng viết và đọc số La Mã trong các bài toán và cuộc sống.
1. Giới thiệu về số La Mã
Số La Mã là một hệ thống ký hiệu số được sử dụng từ thời La Mã cổ đại, bao gồm các ký tự I, V, X, L, C, D, và M. Hệ thống này được sử dụng rộng rãi trong các mặt đồng hồ, sách lịch sử, và các sự kiện.
2. Các ký hiệu số La Mã cơ bản
Các ký tự và giá trị của chúng:
- I: 1
- V: 5
- X: 10
- L: 50
- C: 100
- D: 500
- M: 1,000
3. Quy tắc viết số La Mã
Để viết số La Mã, chúng ta cần tuân theo các quy tắc sau:
- Quy tắc cộng: Nếu một chữ số nhỏ đứng trước chữ số lớn, ta cộng giá trị của chúng. Ví dụ:
- II = 2 (1 + 1)
- XX = 20 (10 + 10)
- Quy tắc trừ: Nếu một chữ số nhỏ đứng trước chữ số lớn, ta trừ giá trị của chữ số nhỏ từ chữ số lớn. Ví dụ:
- IV = 4 (5 - 1)
- IX = 9 (10 - 1)
- Quy tắc lặp lại: Các chữ số I, X, C, M có thể lặp lại tối đa 3 lần. Các chữ số V, L, D không được lặp lại.
4. Cách viết một số La Mã
Ví dụ minh họa cách viết một số La Mã:
- Số 8: VIII (5 + 1 + 1 + 1)
- Số 14: XIV (10 + 5 - 1)
- Số 27: XXVII (10 + 10 + 5 + 1 + 1)
5. Thực hành
- Yêu cầu học sinh viết các số La Mã từ 1 đến 20.
- Yêu cầu học sinh viết số La Mã của các số sau: 15, 30, 48, 99.
6. Tổng kết
Qua bài học này, học sinh đã hiểu được cách viết và đọc số La Mã, cũng như áp dụng quy tắc cộng và trừ trong việc viết các số.
7. Bài Tập, Các em hãy làm các bài tập trên.
Để viết các số La Mã không quá 30 ta dùng 3 ký tự I, V và X(gọi là những số La Mã) ba chữ số đó kết hợp với nhau ta có thể biểu diễn số tự nhiên từ 1 đến 30 như sau:
| Chữ số La Mã | I | V | X |
| Giá trị trong hệ thập phân | 1 | 5 | 10 |
Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I | II | III | IV | V | VI | VII | VIII | IX | X |
Biểu diễn các số từ 11 đến 20 (ta thêm X vào bên trái mỗi số từ 1 đến 10)
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| XI | XII | XIII | XIV | XV | XVI | XVII | XVIII | XIX | XX |
Biểu diễn các số từ 21 đến 30 (ta thêm XX vào bên trái mỗi số từ 1 đến 10)
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| XXI | XXII | XXIII | XXIV | XXV | XXVI | XXVII | XXVIII | XXIX | XXX |
⚠ không có chữ số la mã nào biểu diễn số 0
-
Bài tập: Thứ tự trong tập hợp số tự nhiên
Mục tiêu: Giúp học sinh hiểu rõ hơn về thứ tự của các số tự nhiên và cách sắp xếp chúng từ nhỏ đến lớn, từ lớn đến nhỏ.
Phần 1: Sắp xếp thứ tự
-
Sắp xếp các số sau theo thứ tự tăng dần:
- a) 15, 7, 23, 9, 5
- b) 34, 21, 12, 8, 29
- c) 2, 11, 5, 17, 14
-
Sắp xếp các số sau theo thứ tự giảm dần:
- a) 10, 20, 5, 15, 30
- b) 45, 18, 27, 36, 9
- c) 8, 3, 19, 7, 12
-
Phần 2: Điền vào chỗ trống
-
Điền dấu ">" hoặc "<" vào chỗ trống để biểu thị mối quan hệ thứ tự giữa hai số:
- a) 12 ___ 18
- b) 25 ___ 30
- c) 7 ___ 3
- d) 15 ___ 15
-
Cho dãy số: 2, 4, 6, 8, __, 12. Số cần điền vào chỗ trống là bao nhiêu?
-
Phần 3: Bài toán tình huống
-
Lớp học có 5 bạn: Lan, Mai, Minh, An, và Bình. Số kẹo mỗi bạn có như sau: Lan có 8 viên kẹo, Mai có 3 viên, Minh có 5 viên, An có 10 viên, và Bình có 6 viên.
- a) Sắp xếp tên các bạn theo thứ tự số kẹo từ ít đến nhiều.
- b) Ai có nhiều kẹo nhất? Ai có ít kẹo nhất?
-
Ứng dụng thực tế: Có 3 số nhà trên một con phố: 15, 22 và 9. Sắp xếp các số nhà này từ bé đến lớn.
-
Gợi ý: Các em hãy nhớ rằng trong tập hợp số tự nhiên, số càng lớn thì vị trí càng cao. Số càng nhỏ thì vị trí càng thấp. Sử dụng dấu ">" và "<" để so sánh hai số tự nhiên.
Bài tập này sẽ giúp học sinh rèn luyện khả năng sắp xếp và so sánh các số tự nhiên, cũng như áp dụng vào các tình huống thực tế.
-
Phép nhân và các yếu tố liên quan:
- Thừa số và tích: Phép nhân giữa hai số tự nhiên tạo ra kết quả gọi là tích, với các số được nhân gọi là thừa số.
-
Các tính chất của phép nhân:
- Tính chất giao hoán: Thay đổi vị trí của các thừa số không làm thay đổi kết quả. Ví dụ: a×b=b×aa \times b = b \times aa×b=b×a.
- Tính chất kết hợp: Khi nhân nhiều số, cách kết hợp các số không làm thay đổi kết quả. Ví dụ: (a×b)×c=a×(b×c)(a \times b) \times c = a \times (b \times c)(a×b)×c=a×(b×c).
- Tính chất phân phối của phép nhân đối với phép cộng: Phép nhân phân phối qua phép cộng. Ví dụ: a×(b+c)=(a×b)+(a×c)a \times (b + c) = (a \times b) + (a \times c)a×(b+c)=(a×b)+(a×c).
-
Phép chia:
-
Phép chia hết và phép chia có dư:
- Phép chia hết là khi số bị chia chia cho số chia không dư.
- Phép chia có dư là khi phép chia để lại một phần dư.
-
Các thành phần trong phép chia:
- Số bị chia: Số được chia.
- Số chia: Số dùng để chia.
- Thương: Kết quả của phép chia.
- Số dư: Phần còn lại sau khi chia.
-
Bài tập
- Thực hiện phép nhân hai số tự nhiên.
- Thực hiện phép chia hai số tự nhiên:
- Thực hiện phép chia hết và phép chia có dư.
- Áp dụng tính chất của phép nhân và phép chia trong tính toán:
- Tận dụng các tính chất giao hoán, kết hợp và phân phối để tính nhẩm và tính toán hợp lý.
- Giải quyết các bài toán thực tiễn:
- Sử dụng phép nhân và phép chia số tự nhiên để giải quyết các vấn đề thực tiễn trong cuộc sống hàng ngày, liên quan đến việc tính toán số lượng, phân chia đồ vật, v.v.
Phép nhân thừa số tích
- Tính chất giao hoán kết hợp của phép nhân
- Tính chất phân phối của phép nhân đối với phép cộng
- Phép chia hết, phép chia có dư
- Số bị chia, số chia, thương, số dư
Bài tập:
- Thực hiện phép nhân hai số tự nhiên
- Thực hiện phép chia hai số tự nhiên( chia hết và chia có dư)
- Áp dựng tính chất của phép nhân và phép chia trong tính toán(tính nhẫm, tính hợp lí)
- Giải quyết được những vấn đề thực tiển, gắn với việc thực hiện phép nhân và phép chia số tự nhiên
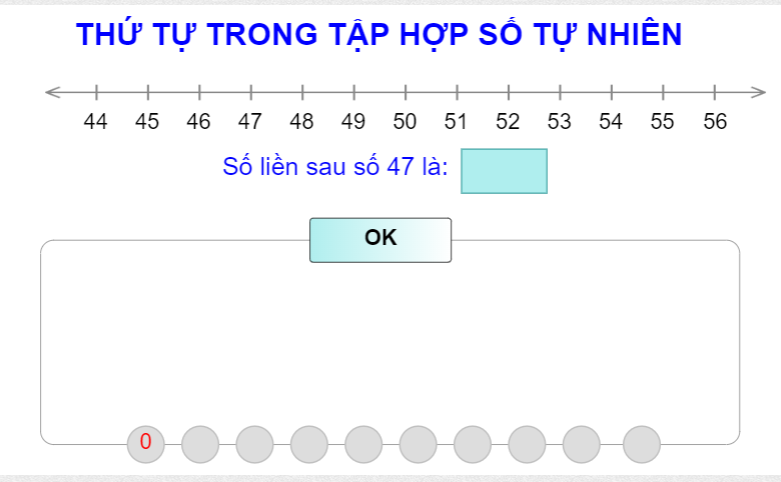
Khái niệm Tia Số
Tia số là một công cụ trực quan dùng để biểu diễn các số tự nhiên theo thứ tự. Trên tia số, các số tự nhiên được sắp xếp từ trái qua phải theo thứ tự tăng dần, bắt đầu từ 0 và tiếp tục tăng lên mà không có điểm kết thúc. Tia số giúp học sinh dễ dàng nhận biết và so sánh các số tự nhiên.
Điểm Biểu Diễn Một Số
Mỗi số tự nhiên trên tia số được biểu diễn bằng một điểm. Ví dụ, điểm 0 là điểm bắt đầu, tiếp theo là 1, 2, 3, và cứ thế cho đến vô hạn. Khoảng cách giữa các điểm này thường được giữ cố định, giúp tạo sự liên tục và dễ nhận diện thứ tự.
Hai Số Tự Nhiên Liên Tiếp
Trên tia số, mỗi số tự nhiên có một số kế tiếp đứng ngay sau nó, gọi là số liền sau. Tương tự, mỗi số (trừ 0) cũng có một số đứng ngay trước nó, gọi là số liền trước. Hai số tự nhiên liên tiếp chỉ cách nhau đúng 1 đơn vị. Chẳng hạn, 3 và 4 là hai số liên tiếp, trong đó 3 là số liền trước của 4, và 4 là số liền sau của 3.
Nhận Biết Thứ Tự trong Tập Hợp Số Tự Nhiên
Tia số giúp chúng ta nhận biết thứ tự của các số tự nhiên một cách trực quan. Số đứng càng xa về bên phải thì càng lớn, và số đứng bên trái sẽ nhỏ hơn. Điều này giúp học sinh hiểu thứ tự sắp xếp của các số tự nhiên trên tia số.
So Sánh Hai Số Tự Nhiên
Để so sánh hai số tự nhiên, chúng ta có thể quan sát vị trí của chúng trên tia số. Số nào nằm bên trái sẽ nhỏ hơn số nằm bên phải. Chẳng hạn, khi so sánh 2 và 5, ta thấy 2 nằm bên trái 5 trên tia số, vì vậy 2<52 < 52<5. Việc sử dụng tia số giúp cho việc so sánh trở nên trực quan và dễ hiểu hơn.
Kết luận
Tia số là một công cụ quan trọng giúp học sinh hiểu rõ về các khái niệm cơ bản của số tự nhiên như điểm biểu diễn số, số liền trước, số liền sau, và cách so sánh thứ tự các số. Qua tia số, học sinh có thể hình dung rõ ràng về cách các số tự nhiên sắp xếp và liên hệ với nhau, từ đó nắm vững các khái niệm cơ bản trong toán học.

Bài 6: Lũy thừa với số mũ tự nhiên
- Lũy thừa
- Cơ số, số mũ
- Bình phương, lập phương
- Thực hiện phép tính nâng lên kuyx thừa với số mũ tự nhiên
- Nhân chia hai lũy thừa cùng cơ số với số mũ tự nhiên
- Giải quyết được vấn đề thực tiễn gắn với thực hiện phép tính lũy thừa với số mũ tự nhiên
Bài 1: Viết các tích sau dưới dạng một lũy thừa
Bài 2: Viết kết quả phép tính sau dưới dạng một lũy thừa
Chú ý: a1 = a
a0 = 1
be|was/were|been|được
beat|beat|beaten|đánh bại
become|became|become|trở thành
begin|began|begun|bắt đầu
bet|bet|bet|đặt cược
bid|bid|bid|thầu
bind|bound|bound|buộc, kết thân
bite|bit|bitten|cắn
blow|blew|blown|thổi
break|broke|broken|đập vỡ
bring|brought|brought|mang lại
broadcast|broadcast|broadcast|phát sóng
build|built|built|xây dựng
buy|bought|bought|mua
catch|caught|caught|bắt
choose|chose|chosen|chọn
come|came|come|đến
cost|cost|cost|phải trả, trị giá
cut|cut|cut|cắt
dig|dug|dug|đào
do|did|done|làm
draw|drew|drawn|vẽ
drink|drank|drunk|uống
drive|drove|driven|lái xe
eat|ate|eaten|ăn
fall|fell|fallen|giảm
feed|fed|fed|cho ăn
feel|felt|felt|cảm thấy
fight|fought|fought|chiến đấu
find|found|found|tìm
fly|flew|flown|bay
forget|forgot|forgotten|quên
forgive|forgave|forgiven|tha thứ
get|got|got/gotten|có được
give|gave|given|cung cấp cho
go|went|gone|đi
grow|grew|grown|phát triển
hang|hung|hung|treo
have|had|had|có
hear|heard|heard|nghe
hide|hid|hidden|ẩn
hit|hit|hit|nhấn
hold|held|held|tổ chức
hurt|hurt|hurt|tổn thương
keep|kept|kept|giữ
know|knew|known|biết
lay|laid|laid|đặt, để
lead|led|led|dẫn
leave|left|left|lại
lend|lent|lent|cho vay
let|let|let|cho phép, để cho
lie|lay|lain|nói dối
lose|lost|lost|mất
make|made|made|làm
meet|met|met|đáp ứng
pay|paid|paid|trả
put|put|put|đặt, để
read|read|read|đọc
ride|rode|ridden|cưỡi (ngựa), đạp (xe)
ring|rang|rung|vòng
rise|rose|risen|tăng
run|ran|run|chạy
run|ran|run|chạy
say|said|said|nói
see|saw|seen|thấy
sell|sold|sold|bán
send|sent|sent|gửi
shut|shut|shut|đóng
sing|sang|sung|hát
sit|sat|sat|ngồi
sleep|slept|slept|ngủ
speak|spoke|spoken|nói
spend|spent|spent|chi tiêu
stand|stood|stood|đứng
sting|stung|stung|chọc tức
swim|swam|swum|bơi
swing|swung|swung|nhún nhảy
take|took|taken|có
teach|taught|taught|dạy
tell|told|told|nói
think|thought|thought|nghĩ
understand|understood|understood|hiểu
wake|woke|woken|thức
wear|wore|worn|mặc
win|won|won|giành chiến thắng
wind|wound|wound|thổi
write|wrote|written|viết
1. Nhắc lại về biểu thức
Các số được nối với nhau bởi dấu các phép tính (cộng, trừ, nhân, chia, nâng lên lũy thừa) làm thành một biểu thức.
Một số cũng được coi là một biểu thức.
Chú ý: Trong một biểu thức có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.
2. Thứ tự thực hiện các phép tính
a) Đối với biểu thức không có dấu ngoặc
- Nếu chỉ có các phép cộng, trừ hoặc chỉ có các phép nhân, chia, ta thực hiện các phép tính theo thứ tự từ trái sang phải.
- Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến phép nhân và phép chia, cuối cùng đến phép cộng và trừ.
b) Đối với biểu thức có dấu ngoặc:
Nếu các biểu thức có các dấu ngoặc: ngoặc tròn (), ngoặc vuông [], ngoặc nhọn {} ta thực hiện theo thứ tự sau:() → [] → {}.
Chú ý: Khi bạn đăng nhập thì điểm được ghi nhận như sau:
- Có 10 câu hỏi
- Đúng 1 câu được cộng 1 điểm
- Sai 1 câu bị trừ 1 điểm
- Làm cho đến khi nào tất cả các câu đều đúng là hoàn thành bài học
Chúc các em học tốt bài học này

Phép chia hết là gì:
Phép chia hết là phép chia có số dư bằng không, các em hiểu đơn giản như vậy thôi.
Ký hiệu chia hết: ⋮
Ký hiệu không chia hết: ⁄⋮
Chú ý bắt buộc đối với phép chia: a chia cho b, b # 0
Các tính chất chia hết của tập hợp:
Dấu hiệu chia hết:
- Tổng: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
- ví dụ a chia hết cho b, c cũng chia hết cho b thì a cộng b cũng chia hết cho c
- Hiệu: Nếu số trừ và số bị trừ đều chia hết cho cùng 1 số thì hiệu chia hết cho số đó
- ví dụ a chia hết cho b, c cũng chia hết cho b thì a trừ b cũng chia hết cho c
- Nhân: Nếu 1 thừa số của tích chia hết cho 1 số thì tích chia hết cho số đó
- ví dụ: a chia hết cho 7 thì 2a cũng chia hết cho 7
Dấu hiệu không chia hết:
- Nếu a chia hết cho m, b không chia hết cho m thì: a+b cũng không chia hết cho m.
- Nếu a chia hết cho m, b không chia hết cho m thì: a-b cũng không chia hết cho m.
Tóm lại: tất cả các số hạng của một biểu thức chia hết cho m thì biểu thức đó chia hết cho m
Mời bạn thực hiện các bài tập trên được ra ngẫu nhiên, đăng nhập để ghi điểm.
Trong toán học, khi nói đến tính chất chia hết của một số cho một số khác, chúng ta thường xem xét các tập hợp số nguyên dương. Các tính chất chia hết này giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các số và cách chúng ta phân tích chúng. Dưới đây là một số tính chất chia hết của tập hợp:
1. Số chẵn và số lẻ
- Một số nguyên dương được gọi là số chẵn nếu nó chia hết cho 2 mà không dư.
- Một số nguyên dương được gọi là số lẻ nếu nó không chia hết cho 2 mà vẫn là số nguyên.
Sự phân loại giữa số chẵn và số lẻ giúp chúng ta dễ dàng nhận biết và xử lý các bài toán liên quan đến tính chất chia hết.
2. Số nguyên tố và số hợp
- Một số nguyên dương được gọi là số nguyên tố nếu nó chỉ chia hết cho 1 và chính nó.
- Một số nguyên dương được gọi là số hợp nếu nó có thể chia hết cho các số khác ngoài 1 và chính nó.
Việc hiểu rõ về số nguyên tố và số hợp giúp chúng ta phân tích các số thành các yếu tố cơ bản và áp dụng vào việc giải các bài toán phức tạp hơn.
3. Số hoàn hảo
- Một số nguyên dương được gọi là số hoàn hảo nếu tổng các ước số của nó (không kể chính nó) bằng chính nó.
Số hoàn hảo là một khái niệm quan trọng trong lĩnh vực tính chất chia hết, và chúng ta thường gặp các bài toán liên quan đến số hoàn hảo trong thực tế.
Tính chất chia hết
Khi nói đến tính chất chia hết của các số, chúng ta thường xem xét các phép chia và cách chúng ta xác định được sự chia hết giữa các số. Dưới đây là một số tính chất chia hết quan trọng:
1. Tính chất chia hết cho 2
- Một số nguyên dương chia hết cho 2 nếu và chỉ nếu chữ số cuối cùng của số đó là 0, 2, 4, 6, hoặc 8.
Ví dụ: 24, 56, 108 là các số chia hết cho 2 vì chữ số cuối cùng của chúng là 4, 6, 8.
2. Tính chất chia hết cho 3
- Một số nguyên dương chia hết cho 3 nếu và chỉ nếu tổng các chữ số của số đó chia hết cho 3.
Ví dụ: 123 (1+2+3=6), 369 (3+6+9=18) là các số chia hết cho 3.
3. Tính chất chia hết cho 5
- Một số nguyên dương chia hết cho 5 nếu và chỉ nếu chữ số cuối cùng của số đó là 0 hoặc 5.
Ví dụ: 35, 120, 555 là các số chia hết cho 5 vì chữ số cuối cùng của chúng là 5 hoặc 0.
4. Tính chất chia hết cho 9
- Một số nguyên dương chia hết cho 9 nếu và chỉ nếu tổng các chữ số của số đó chia hết cho 9.
Ví dụ: 81 (8+1=9), 135 (1+3+5=9) là các số chia hết cho 9.
Tính chất chia hết của một tích
Khi nói đến tính chất chia hết của một tích, chúng ta xem xét cách mà các số trong tích ảnh hưởng đến việc chia hết của tích đó. Dưới đây là một số tính chất quan trọng:
1. Tính chất chia hết của tích
- Nếu một số chia hết cho một số nguyên dương a và cũng chia hết cho một số nguyên dương b, thì nó chia hết cho tích của a và b.
Ví dụ: Nếu một số chia hết cho cả 3 và 4, thì nó chia hết cho 3x4=12.
2. Tính chất chia hết của các ước số
- Nếu một số chia hết cho một số nguyên dương a và b, thì nó cũng chia hết cho ước số chung lớn nhất của a và b.
Ví dụ: Nếu một số chia hết cho cả 6 và 9, thì nó chia hết cho ƯCLN(6,9)=3.
3. Tính chất chia hết của tích các số nguyên tố
- Nếu một số chia hết cho một tích các số nguyên tố a và b, thì nó chia hết cho cả a và b.
Ví dụ: Nếu một số chia hết cho 2x3=6, thì nó chia hết cho cả 2 và 3.
Tính chất của phép chia
Khi thực hiện phép chia giữa hai số, chúng ta cần hiểu rõ về các tính chất của phép chia để có thể giải quyết các bài toán liên quan đến chia hết. Dưới đây là một số tính chất quan trọng:
1. Tính chất của phép chia hết
- Nếu một số chia hết cho một số nguyên dương a và b, thì phần dư khi chia số đó cho tích của a và b sẽ bằng 0.
Ví dụ: Nếu một số chia hết cho cả 4 và 6, thì phần dư khi chia cho 4x6=24 sẽ bằng 0.
2. Tính chất của phép chia cho 1
- Mọi số nguyên dương đều chia hết cho 1 và phần dư khi chia cho 1 luôn bằng 0.
Đây là một tính chất cơ bản của phép chia mà chúng ta thường sử dụng trong các bài toán toán học hàng ngày.
3. Tính chất của phép chia cho chính nó
- Một số nguyên dương chia cho chính nó sẽ luôn có phần dư bằng 0.
Ví dụ: 7 chia cho 7 sẽ có phần dư bằng 0.
Kết luận
Trên đây là một số tính chất chia hết quan trọng mà chúng ta cần nắm vững khi học và áp dụng trong toán học. Việc hiểu rõ về các tính chất này sẽ giúp chúng ta giải quyết các bài toán phức tạp và phát triển kỹ năng suy luận logic. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về chủ đề này. Nếu còn câu hỏi hoặc cần thêm thông tin, đừng ngần ngại để lại comment để chúng tôi hỗ trợ bạn nhé. Chúc bạn học tốt!
Trên thế giới toán học, việc nắm vững các dấu hiệu chia hết cho 2 và cho 5 là rất quan trọng. Để giúp bạn hiểu rõ hơn về chủ đề này, bài viết sau sẽ cung cấp thông tin chi tiết về dấu hiệu chia hết cho 2 và cho 5, những số chia hết cho chúng, phép thử chia hết, ứng dụng của dấu hiệu chia hết cho 2 và cho 5, cũng như sự liên hệ giữa chúng. Cuối bài viết là một số bài tập để bạn ôn tập và kiểm tra kiến thức của mình.
Dấu hiệu chia hết cho 2
Những số chia hết cho 2
Số chia hết cho 2 là những số mà khi chia cho 2 thì có số dư bằng 0. Cụ thể, nếu số a chia hết cho 2, ta có thể biểu diễn được như sau: a = 2k (với k là số nguyên). Ví dụ, các số 2, 4, 6, 8, 10, ... đều chia hết cho 2 vì khi chia cho 2 không còn số dư.
Phép thử chia hết cho 2
Để kiểm tra xem một số có chia hết cho 2 hay không, ta chỉ cần xem chữ số cuối cùng của số đó. Nếu chữ số cuối cùng là 0, 2, 4, 6 hoặc 8 thì số đó chia hết cho 2. Ví dụ, số 123456 chia hết cho 2 vì chữ số cuối cùng là 6.
Ứng dụng của dấu hiệu chia hết cho 2
Dấu hiệu chia hết cho 2 được áp dụng rộng rãi trong các bài toán về tổ hợp, xác suất và lý thuyết đồ thị. Việc nắm vững dấu hiệu này giúp chúng ta giải quyết các bài toán một cách nhanh chóng và chính xác hơn.
Dấu hiệu chia hết cho 5
Những số chia hết cho 5
Số chia hết cho 5 là những số mà khi chia cho 5 thì có số dư bằng 0. Tức là nếu số b chia hết cho 5, ta có thể biểu diễn được như sau: b = 5m (với m là số nguyên). Ví dụ, các số 5, 10, 15, 20, 25, ... đều chia hết cho 5 vì khi chia cho 5 không còn số dư.
Phép thử chia hết cho 5
Để kiểm tra xem một số có chia hết cho 5 hay không, ta chỉ cần xem chữ số cuối cùng của số đó. Nếu chữ số cuối cùng là 0 hoặc 5 thì số đó chia hết cho 5. Ví dụ, số 12345 chia hết cho 5 vì chữ số cuối cùng là 5.
Ứng dụng của dấu hiệu chia hết cho 5
Dấu hiệu chia hết cho 5 cũng được áp dụng trong nhiều lĩnh vực khác nhau của toán học như hình học, số học và đại số. Việc hiểu rõ về dấu hiệu này giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả.
Sự liên hệ giữa dấu hiệu chia hết cho 2 và dấu hiệu chia hết cho 5
Dấu hiệu chia hết cho 2 và dấu hiệu chia hết cho 5 là hai khái niệm cơ bản trong toán học. Mặc dù chúng có tính chất riêng biệt, nhưng đôi khi chúng có thể được kết hợp để giải quyết các bài toán phức tạp hơn. Ví dụ, nếu một số chia hết cho cả 2 và 5, tức là số đó chia hết cho 10. Sự liên hệ giữa dấu hiệu chia hết cho 2 và 5 giúp chúng ta hiểu rõ hơn về tính chất của các số tự nhiên.
Bài tập về dấu hiệu chia hết cho 2 và cho 5
Để kiểm tra kiến thức của mình về dấu hiệu chia hết cho 2 và cho 5, bạn có thể thử giải các bài tập sau:
- Hãy liệt kê tất cả các số chia hết cho cả 2 và 5 trong khoảng từ 1 đến 100.
- Cho số nguyên dương n = 123456789. Hỏi n chia hết cho 2 hay không?
- Tìm số lớn nhất có 6 chữ số chia hết cho 5.
- Chứng minh rằng nếu một số chia hết cho 2 và 5 thì số đó chia hết cho 10.
Hãy tự thử sức và kiểm tra đáp án sau:
- Các số chia hết cho cả 2 và 5 trong khoảng từ 1 đến 100 là 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
- Số n = 123456789 không chia hết cho 2 vì chữ số cuối cùng là 9.
- Số lớn nhất có 6 chữ số chia hết cho 5 là 999990.
- Nếu một số chia hết cho cả 2 và 5, tức là chia hết cho 10.
Kết luận
Qua bài viết trên, hy vọng bạn đã hiểu rõ hơn về dấu hiệu chia hết cho 2 và cho 5, những số chia hết cho chúng, phép thử chia hết, ứng dụng của dấu hiệu chia hết cho 2 và cho 5, cũng như sự liên hệ giữa chúng. Hãy ôn tập và áp dụng kiến thức này vào việc giải các bài toán toán học để nâng cao kỹ năng của mình. Chúc bạn thành công!

Trong toán học, việc hiểu và áp dụng các quy tắc chia hết là một kỹ năng quan trọng giúp chúng ta giải quyết các bài toán phức tạp một cách nhanh chóng và chính xác. Trên thực tế, có những quy tắc đơn giản giúp chúng ta xác định được một số tổng quát về việc chia hết cho các số nguyên như 3 và 9. Trên thực tế, việc áp dụng các quy tắc này không chỉ giúp chúng ta trong việc tính toán mà còn giúp rèn luyện tư duy logic và khả năng suy luận. Trong bài viết này, chúng ta sẽ cùng thực hành kỹ năng chia hết cho 3 và cho 9 để nắm vững hơn về chủ đề này.
Chia hết cho 3
Quy tắc chia hết cho 3
Khi một số tự nhiên chia hết cho 3, tổng các chữ số của số đó cũng chia hết cho 3. Đây là một quy tắc đơn giản giúp chúng ta kiểm tra xem một số có chia hết cho 3 hay không một cách nhanh chóng. Ví dụ, số 123 (1 + 2 + 3 = 6) chia hết cho 3 vì tổng các chữ số là 6.
Ví dụ minh họa
Để hiểu rõ hơn về quy tắc chia hết cho 3, chúng ta cùng xem qua một ví dụ minh họa sau đây:
| Số ban đầu | Tổng các chữ số | Kết quả |
|---|---|---|
| 246 | 2 + 4 + 6 = 12 | Chia hết cho 3 |
| 357 | 3 + 5 + 7 = 15 | Chia hết cho 3 |
| 489 | 4 + 8 + 9 = 21 | Chia hết cho 3 |
Như vậy, từ các ví dụ trên, chúng ta có thể thấy rằng nếu tổng các chữ số của một số là một bội số của 3 thì số đó sẽ chia hết cho 3.
Chia hết cho 9
Quy tắc chia hết cho 9
Tương tự như quy tắc chia hết cho 3, khi một số tự nhiên chia hết cho 9, tổng các chữ số của số đó cũng chia hết cho 9. Điều này giúp chúng ta kiểm tra một cách dễ dàng xem một số có chia hết cho 9 hay không. Ví dụ, số 135 (1 + 3 + 5 = 9) chia hết cho 9 vì tổng các chữ số là 9.
Ví dụ minh họa
Chúng ta cùng xem qua một số ví dụ minh họa để hiểu rõ hơn về quy tắc chia hết cho 9:
| Số ban đầu | Tổng các chữ số | Kết quả |
|---|---|---|
| 234 | 2 + 3 + 4 = 9 | Chia hết cho 9 |
| 567 | 5 + 6 + 7 = 18 | Chia hết cho 9 |
| 891 | 8 + 9 + 1 = 18 | Chia hết cho 9 |
Từ các ví dụ trên, chúng ta có thể thấy rằng nếu tổng các chữ số của một số là một bội số của 9 thì số đó sẽ chia hết cho 9.
Áp dụng vào thực hành
Bài tập về chia hết cho 3
Để rèn luyện kỹ năng chia hết cho 3, chúng ta có thể thực hành qua các bài tập sau:
- Hãy kiểm tra xem các số sau đây có chia hết cho 3 không: 126, 258, 369.
- Tìm số tự nhiên nhỏ nhất có ba chữ số chia hết cho 3.
- Cho số n = 123456789. Tính tổng các chữ số của số n.
Dưới đây là bảng kết quả của các bài tập trên:
| Câu hỏi | Kết quả |
|---|---|
| 1. Kiểm tra chia hết cho 3: 126, 258, 369 | Có, Không, Có |
| 2. Số tự nhiên nhỏ nhất chia hết cho 3 có ba chữ số | 102 |
| 3. Tính tổng các chữ số của số n = 123456789 | 45 |
Bài tập về chia hết cho 9
Để thực hành kỹ năng chia hết cho 9, chúng ta có thể giải các bài tập sau:
- Kiểm tra xem các số sau đây có chia hết cho 9 không: 189, 297, 405.
- Tìm số tự nhiên nhỏ nhất có ba chữ số chia hết cho 9.
- Cho số n = 987654321. Tính tổng các chữ số của số n.
Dưới đây là bảng kết quả của các bài tập về chia hết cho 9:
| Câu hỏi | Kết quả |
|---|---|
| 1. Kiểm tra chia hết cho 9: 189, 297, 405 | Có, Có, Không |
| 2. Số tự nhiên nhỏ nhất chia hết cho 9 có ba chữ số | 108 |
| 3. Tính tổng các chữ số của số n = 987654321 | 45 |
Kết luận
Trong bài viết này, chúng ta đã cùng thực hành kỹ năng chia hết cho 3 và cho 9 thông qua việc áp dụng quy tắc đơn giản về tổng các chữ số của một số. Việc nắm vững quy tắc này không chỉ giúp chúng ta trong việc kiểm tra tính chia hết mà còn rèn luyện tư duy logic và khả năng suy luận. Hy vọng rằng bài viết này sẽ giúp ích cho bạn trong quá trình học tập và rèn luyện kỹ năng toán học của mình.

Trong toán học, bội số và ước số là hai khái niệm cơ bản mà học sinh lớp 6 thường gặp phải. Việc hiểu rõ về bội số và ước số không chỉ giúp học sinh giải các bài toán một cách dễ dàng mà còn áp dụng vào cuộc sống hàng ngày. Bài viết này sẽ giúp bạn hiểu rõ hơn về bội số và ước số thông qua các quy tắc, bài toán và ứng dụng của chúng.
Bội số là gì?
Định nghĩa
Bội số của một số là kết quả của việc nhân số đó với một số nguyên dương bất kỳ. Nói cách khác, bội số là các số mà khi chia hết cho số ban đầu thì được một số nguyên dương.
Quy tắc tìm bội số của một số
Để tìm bội số của một số, chúng ta có thể nhân số đó với các số nguyên dương từ 1 trở đi và liệt kê các kết quả. Ví dụ, bội số của 5 là: 5, 10, 15, 20, ...
Bài toán về bội số
Hãy tính bội số chung nhỏ nhất của 6 và 8.
| Số | Bội số của số 6 | Bội số của số 8 |
|---|---|---|
| 1 | 6 | 8 |
| 2 | 12 | 16 |
| 3 | 18 | 24 |
| 4 | 24 | 32 |
| 5 | 30 | 40 |
| ... | ... | ... |
Từ bảng trên, ta thấy bội số chung nhỏ nhất của 6 và 8 là 24.
Ước số là gì?
Định nghĩa
Ước số của một số là các số tự nhiên mà khi chia số đó cho các số đó thì được một số nguyên dương.
Quy tắc tìm ước số của một số
Để tìm ước số của một số, chúng ta có thể chia số đó cho các số tự nhiên từ 1 trở đi và liệt kê các ước số. Ví dụ, ước số của 12 là: 1, 2, 3, 4, 6, 12.
Bài toán về ước số
Hãy tính ước số chung lớn nhất của 24 và 36.
| Số | Ước số của số 24 | Ước số của số 36 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 6 | 6 | 6 |
| 8 | 8 | 8 |
| 12 | 12 | 12 |
| 24 | 24 | 24 |
| 36 |
Từ bảng trên, ta thấy ước số chung lớn nhất của 24 và 36 là 12.
Quy tắc tìm bội số của một số
Để tìm bội số của một số, chúng ta có thể áp dụng các quy tắc sau:
- Nhân số đó với các số nguyên dương từ 1 trở đi: Bội số của một số sẽ bao gồm chính số đó và các bội số của nó.
- Liệt kê các bội số và tìm ra bội số chung nhỏ nhất: Để tìm bội số chung nhỏ nhất của hai số, chúng ta cần liệt kê các bội số của từng số và chọn ra bội số chung nhỏ nhất.
Quy tắc tìm ước số của một số
Để tìm ước số của một số, chúng ta có thể áp dụng các quy tắc sau:
- Chia số đó cho các số tự nhiên từ 1 trở đi: Ước số của một số sẽ bao gồm chính số đó và các ước số của nó.
- Liệt kê các ước số và tìm ra ước số chung lớn nhất: Để tìm ước số chung lớn nhất của hai số, chúng ta cần liệt kê các ước số của từng số và chọn ra ước số chung lớn nhất.
Bài toán về bội số và ước số
Hãy xem xét một bài toán về bội số và ước số để hiểu rõ hơn về cách áp dụng kiến thức này:
Bài toán: Tìm bội số chung nhỏ nhất của 9 và 15.
Giải pháp:
- Bội số của 9: 9, 18, 27, 36, 45, ...
- Bội số của 15: 15, 30, 45, 60, ...
Ta thấy bội số chung nhỏ nhất của 9 và 15 là 45.
Ứng dụng của bội số và ước số trong cuộc sống
Bội số và ước số không chỉ là khái niệm trong sách giáo khoa mà còn được áp dụng trong nhiều lĩnh vực trong cuộc sống hàng ngày. Dưới đây là một số ví dụ về việc áp dụng bội số và ước số:
- Sắp xếp thời gian: Khi bạn muốn biết thời gian cần để hoàn thành một công việc dựa trên bội số của thời gian làm việc của bạn và của đồng nghiệp.
- Quản lý tài chính: Áp dụng ước số để phân tích chi tiêu hàng tháng và tìm ra cách tiết kiệm hiệu quả.
- Thiết kế lịch trình: Sử dụng bội số để xác định thời gian di chuyển giữa các địa điểm và lập kế hoạch đi lại một cách hợp lý.
Thực hành tìm bội số và ước số
Để nắm vững kiến thức về bội số và ước số, hãy thực hành các bài tập sau:
Bài tập 1: Tìm bội số chung nhỏ nhất của 12 và 18.
Giải pháp:
- Bội số của 12: 12, 24, 36, 48, ...
- Bội số của 18: 18, 36, 54, 72, ...
Ta thấy bội số chung nhỏ nhất của 12 và 18 là 36.
Bài tập 2: Tìm ước số chung lớn nhất của 20 và 30.
Giải pháp:
- Ước số của 20: 1, 2, 4, 5, 10, 20
- Ước số của 30: 1, 2, 3, 5, 6, 10, 15, 30
Ta thấy ước số chung lớn nhất của 20 và 30 là 10.
Mẹo nhớ về bội số và ước số
Để dễ dàng nhớ về bội số và ước số, hãy áp dụng những mẹo sau:
- Bội số: Bội số luôn lớn hơn hoặc bằng số gốc.
- Ước số: Ước số luôn nhỏ hơn hoặc bằng số gốc.
Trắc nghiệm kiến thức về bội số và ước số
Hãy kiểm tra kiến thức của bạn với các câu hỏi sau:
- Bội số chung nhỏ nhất của 4 và 6 là bao nhiêu?
- Ước số chung lớn nhất của 15 và 25 là bao nhiêu?
- Liệt kê các bội số của 7.
- Tìm ước số của 18.
- Bội số chung nhỏ nhất của 9 và 12 là bao nhiêu?
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về bội số và ước số trong toán học lớp 6. Việc nắm vững kiến thức về bội số và ước số không chỉ giúp học sinh giải các bài tập một cách dễ dàng mà còn áp dụng vào cuộc sống hàng ngày. Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về hai khái niệm quan trọng này.

Số nguyên tố
Trước khi đi vào tìm hiểu về các phép tính cơ bản, chúng ta cần nắm vững một khái niệm rất quan trọng trong toán học đó là số nguyên tố. Số nguyên tố là các số tự nhiên chỉ có hai ước số là 1 và chính nó. Ví dụ: số 2, 3, 5, 7... đều là các số nguyên tố. Trong khi đó, các số như 4, 6, 8, 10... không phải là số nguyên tố vì chúng có thể được phân tích thành tích của các số khác.
Đây là một khái niệm quan trọng không chỉ trong toán học mà còn trong các lĩnh vực khác như mã hóa, khoa học máy tính và kinh tế. Việc hiểu và áp dụng các tính chất của số nguyên tố sẽ giúp chúng ta hiểu sâu hơn về các phép tính cơ bản và giải quyết các bài toán liên quan đến chúng.
Hợp số
Hợp số là các số tự nhiên có hơn hai ước số. Ví dụ: số 4 có ba ước số là 1, 2 và 4 nên nó không phải là số nguyên tố mà là một số hợp số. Một số khác có thể chia hết cho 4 là số 8, có năm ước số là 1, 2, 4, 8. Tương tự, các số như 6, 10, 12... cũng là các số hợp số vì chúng có nhiều hơn hai ước số.
Việc phân biệt các số nguyên tố và hợp số là rất quan trọng trong các bài toán liên quan đến phân tích số. Thông thường, chúng ta cần phân tích một số thành tích các số nguyên tố để giải quyết các bài toán. Việc hiểu về số nguyên tố và hợp số sẽ giúp chúng ta làm việc hiệu quả và chính xác hơn.
Tóm lại các em cần nhớ:
Số nguyên tố là những số tự nhiên lớn hơn 1 và chỉ có 2 ước số dương là 1 và chính nó. Đây là một khái niệm quan trọng trong toán học và thường được giảng dạy từ cấp độ toán lớp 6. Trong bài viết này, chúng ta sẽ tìm hiểu cách tính số nguyên tố và một số đặc điểm quan trọng của chúng.
-
Số nguyên tố là gì? Số nguyên tố là những số tự nhiên mà chỉ có hai ước số dương là 1 và chính nó. Ví dụ, số 2, 3, 5, 7 là các số nguyên tố vì chúng không thể được phân tích thành tích của hai số tự nhiên dương khác.
-
Cách tính số nguyên tố Để kiểm tra xem một số có phải là số nguyên tố hay không, chúng ta có thể sử dụng phương pháp kiểm tra qua các ước số của nó. Nếu số đó chỉ có hai ước số dương là 1 và chính nó, thì đó là số nguyên tố. Ví dụ, để kiểm tra xem số 7 có phải là số nguyên tố hay không, chúng ta sẽ thấy rằng 7 chỉ có hai ước số là 1 và 7 nên đúng là số nguyên tố.
-
Đặc điểm của số nguyên tố
- Số nguyên tố không thể được phân tích thành tích của hai số nguyên dương khác.
- Số nguyên tố luôn lớn hơn 1.
- Số nguyên tố chỉ có hai ước số dương là 1 và chính nó.
Trên đây là một số thông tin cơ bản về số nguyên tố và cách tính chúng. Hy vọng rằng bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm số nguyên tố trong toán học.
Và làm bài tập trên
Chúc các em học tốt
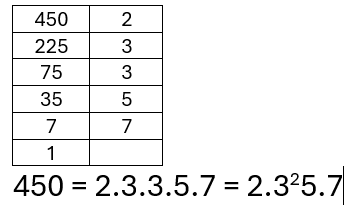
Phân tích một số ra thừa số nguyên tố
Tìm hiểu về các số nguyên tố và phân tích ra thừa số nguyên tố
Số nguyên tố là những số tự nhiên chỉ chia hết cho 1 và chính nó. Phân tích một số ra thừa số nguyên tố là quá trình tìm các số nguyên tố nhỏ nhất mà khi nhân lại với nhau sẽ ra số cần phân tích. Đây là một phương pháp quan trọng trong toán học và có nhiều ứng dụng trong thực tế.
Cách phân tích một số ra thừa số nguyên tố
Ta có thể phân tích theo chiều dọc như sau:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Ví dụ về phân tích số nguyên tố
Ví dụ, để phân tích số 24 ra thừa số nguyên tố, ta có thể chia lần lượt cho các số nguyên tố nhỏ nhất là 2, 3 và 2. Kết quả cuối cùng sẽ là 2 x 2 x 2 x 3 = 24.
| 24 | 2 |
| 12 | 2 |
| 6 | 2 |
| 3 | 3 |
| 1 |
Ứng dụng của phân tích ra thừa số nguyên tố
Phân tích ra thừa số nguyên tố không chỉ giúp chúng ta hiểu rõ hơn về cấu trúc của một số mà còn có thể áp dụng trong việc giải các bài toán toán học phức tạp, trong lĩnh vực mã hóa thông tin, và nhiều lĩnh vực khác.
Kết luận
Phân tích một số ra thừa số nguyên tố là một phương pháp quan trọng trong toán học và mang lại nhiều ứng dụng trong thực tế. Qua bài viết này, hy vọng bạn đã hiểu thêm về quá trình này và cách áp dụng nó trong cuộc sống hàng ngày.

Tìm Ước Số Chung và Bội Số Chung - Cơ Bản Nhưng Quan Trọng
Trong toán học, việc hiểu và áp dụng khái niệm về ước số chung và bội số chung là rất quan trọng. Đặc biệt, trong việc giải các bài toán và làm các bài tập, kiến thức về ước số chung và bội số chung thường xuyên được áp dụng. Hãy cùng nhau tìm hiểu cách tính và áp dụng chúng trong bài toán dưới đây.
Ước Số Chung (USC)
Ước số chung của hai hoặc nhiều số là số tự nhiên lớn nhất mà các số đó đều chia hết cho nó.
Ví dụ: Ước số chung của 12 và 18 là 6, vì 6 là số lớn nhất mà cả 12 và 18 đều chia hết cho nó.
Bội Số Chung (BSC)
Bội số chung của hai hoặc nhiều số là số tự nhiên nhỏ nhất mà tất cả các số đó đều chia hết cho nó.
Ví dụ: Bội số chung của 4 và 6 là 12, vì 12 là số nhỏ nhất mà cả 4 và 6 đều chia hết cho nó.
Cách Tìm Ước Số Chung và Bội Số Chung
Để tìm ước số chung và bội số chung, chúng ta có thể sử dụng phương pháp sau đây:
-
Tìm Ước Số Chung (USC):
- Phân tích mỗi số ra thừa số nguyên tố.
- Chọn ra các thừa số nguyên tố chung.
- Lập tích các tích thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
- Tích đó là ƯCLN phải tìm.
- Ví dụ: Tìm ƯCLN(12, 30)
12 = 2 x 2 x 3
30 = 2 x 3 x 5
Ta có: các thừa số nguyên tố chung là 2 và 3.
Vậy ƯCLN(12, 30) = 2 x 3 = 6
- Ví dụ: Tìm ƯCLN(12, 30)
-
Tìm Bội Số Chung (BSC):
- Liệt kê tất cả các bội số của các số đó.
- Chọn bội số chung nhỏ nhất trong các số đó.
- Nhân bội số chung nhỏ nhất với 1,2... ta được tập hợp bội số chung
- Ví dụ Tìm BCNN(20;54)
Giải:
20=22.5
54 = 2.33
BCNN(20;54)= 22. 33.5=540 - Ta nhân bộ số chung nhỏ nhất 540, 540x2, 540x3 ta được tập hợp bội số chung
- Ví dụ Tìm BCNN(20;54)
Ví dụ về Bài Toán Áp Dụng
Bây giờ, hãy giải một bài toán thực tế để hiểu rõ hơn về cách áp dụng ước số chung và bội số chung.
Bài toán: Hãy tìm ước số chung và bội số chung của các số 24 và 36.
Giải pháp:
-
Ước số chung (USC):
- Ước số chung của 24 và 36 là 12, vì 12 là số lớn nhất mà cả 24 và 36 đều chia hết cho nó.
-
Bội số chung (BSC):
- Bội số chung của 24 và 36 là 72, vì 72 là số nhỏ nhất mà cả 24 và 36 đều chia hết cho nó.
Như vậy, ước số chung của 24 và 36 là 12 và bội số chung của chúng là 72.
Kết Luận
Khái niệm về ước số chung và bội số chung không chỉ đơn giản mà còn rất quan trọng trong toán học. Việc hiểu và áp dụng chúng sẽ giúp chúng ta giải quyết các bài toán và tìm ra những giải pháp chính xác. Chúc các bạn thành công trong việc học tập và rèn luyện kỹ năng toán học!