Toán - Lớp 6
20 bài học toán lớp 6 hàng đầu dành cho học sinh trên toàn quốc!
Tại gogoedu học toán lớp 6, chúng tôi hiểu rằng Toán học là một trong những môn học cốt lõi, có vai trò quan trọng trong sự phát triển tư duy và kỹ năng giải quyết vấn đề của học sinh. Chính vì vậy, chúng tôi đã phát triển một nền tảng học toán trực tuyến đặc biệt dành riêng cho học sinh lớp 6, giúp các em tiếp cận và yêu thích môn học này hơn bao giờ hết.
Tại sao chọn nền tản này để học toán lớp 6?
- Nội dung phong phú, bám sát chương trình học: Tất cả các bài học và bài tập trên website đều được thiết kế dựa trên chương trình học toán lớp 6 chính thức và cập nhật mới nhất, giúp các em không chỉ học tốt mà còn học đúng trọng tâm.
- Sách Toán lớp 6 trong bộ sách giáo khoa "Kết nối tri thức" được biên soạn với mục tiêu phát triển phẩm chất và năng lực của học sinh. Chúng tôi đặc biệt chú trọng đến việc rèn luyện kỹ năng và kết nối kiến thức toán học với các tình huống thực tiễn, giúp các em không chỉ hiểu bài một cách lý thuyết mà còn có thể giải quyết các vấn đề thực tế một cách sáng tạo.
- Toán lớp 6 không chỉ là một cuốn sách; nó là người bạn đồng hành trong hành trình khám phá thế giới số học. Với phương pháp trình bày phong phú và lôi cuốn, sách được thiết kế theo cách thân thiện và hấp dẫn, giúp các em tiếp cận môn Toán một cách tự nhiên và thú vị.
- Ngoài ra, "Toán lớp 6" sẽ cùng các em khám phá vẻ đẹp của toán học, qua đó nuôi dưỡng niềm đam mê và tình yêu với môn học này. Chúng tôi tin rằng, với sự đồng hành của trang web GogoEdu, các em sẽ không chỉ học tốt mà còn yêu thích Toán học hơn.
- Công cụ học tập tiên tiến: Sử dụng công nghệ giáo dục mới nhất, GogoEdu cung cấp các công cụ tương tác giúp học toán trở nên dễ dàng và thú vị hơn. Các tính năng tương tác trực truyến, thảo luận, góp ý, video giảng dạy sinh động và hệ thống đánh giá tự động sẽ giúp các em nắm bắt kiến thức một cách hiệu quả.
- Hỗ trợ tận tâm: Đội ngũ giáo viên dày dạn kinh nghiệm và nhiệt tình sẵn sàng hỗ trợ các em qua các buổi học trực tiếp, diễn đàn trực tuyến và phản hồi bài tập, đảm bảo rằng mọi thắc mắc đều được giải đáp kịp thời.
- Học mọi lúc, mọi nơi: Với GogoEdu, các em có thể học toán mọi lúc mọi nơi, chỉ cần có kết nối internet. Dù ở nhà hay di chuyển, học tập không còn gián đoạn.
Hãy để chúng tôi đồng hành cùng các em trong hành trình chinh phục toán lớp 6, khai phá tiềm năng và phát triển toàn diện. Học ngay hôm nay để trải nghiệm một môi trường học tập chuyên nghiệp, hiện đại và cực kỳ thân thiện!
Hãy khám phá những bài học sau đây - Nơi khởi nguồn của những nhà toán học tương lai!
Bài Tập Toán Lớp 6: Cộng, Trừ Hai Số Nguyên
Mục tiêu:
- Học sinh hiểu và thực hiện được phép cộng, trừ hai số nguyên.
- Học sinh hiểu tính chất của phép cộng hai số nguyên.
- Học sinh nắm vững quy tắc dấu ngoặc.
Nội dung bài học:
Phần 1: Cộng Hai Số Nguyên
-
Cộng hai số nguyên cùng dấu
- Khi cộng hai số nguyên cùng dấu, ta cộng hai giá trị tuyệt đối của chúng và giữ nguyên dấu.
- Ví dụ:
- 5+3=85+3=8
- −4+(−6)=−10−4+(−6)=−10
-
Cộng hai số nguyên khác dấu
- Khi cộng hai số nguyên khác dấu, ta trừ giá trị tuyệt đối nhỏ hơn từ giá trị tuyệt đối lớn hơn và giữ dấu của số có giá trị tuyệt đối lớn hơn.
- Ví dụ:
- 7+(−2)=57+(−2)=5
- −5+8=3−5+8=3
Phần 2: Tính Chất của Phép Cộng Hai Số Nguyên
-
Tính giao hoán
- 𝑎+𝑏=𝑏+𝑎a+b=b+a
- Ví dụ: 3+(−5)=−5+33+(−5)=−5+3
-
Tính kết hợp
- (𝑎+𝑏)+𝑐=𝑎+(𝑏+𝑐)(a+b)+c=a+(b+c)
- Ví dụ: (2+3)+4=2+(3+4)(2+3)+4=2+(3+4)
-
Phần tử 0
- 𝑎+0=𝑎a+0=a
- Ví dụ: −7+0=−7−7+0=−7
Phần 3: Phép Trừ Hai Số Nguyên
-
Khái niệm
- Phép trừ hai số nguyên là phép cộng số đối của số bị trừ.
- 𝑎−𝑏=𝑎+(−𝑏)a−b=a+(−b)
- Ví dụ:
- 5−3=5+(−3)=25−3=5+(−3)=2
- −4−6=−4+(−6)=−10−4−6=−4+(−6)=−10
-
Bài tập thực hành
- Tính các phép trừ sau:
- 8−58−5
- −3−4−3−4
- 7−(−2)7−(−2)
- −6−(−3)−6−(−3)
- Tính các phép trừ sau:
Phần 4: Quy Tắc Dấu Ngoặc
-
Quy tắc dấu ngoặc
- Khi bỏ dấu ngoặc, nếu trước dấu ngoặc là dấu “-” thì ta đổi dấu tất cả các số hạng trong ngoặc.
- Khi bỏ dấu ngoặc, nếu trước dấu ngoặc là dấu “+” thì ta giữ nguyên dấu tất cả các số hạng trong ngoặc.
- Ví dụ:
- −(𝑎+𝑏)=−𝑎−𝑏−(a+b)=−a−b
- −(𝑎−𝑏)=−𝑎+𝑏−(a−b)=−a+b
- +(𝑎+𝑏)=𝑎+𝑏+(a+b)=a+b
-
Bài tập thực hành
- Bỏ dấu ngoặc và tính giá trị các biểu thức sau:
- −(3+5)−(3+5)
- −(−7+2)−(−7+2)
- +(4−6)+(4−6)
- −(−8−3)−(−8−3)
- Bỏ dấu ngoặc và tính giá trị các biểu thức sau:
Phần 5: Bài Tập Tổng Hợp
-
Bài tập lý thuyết
- Giải thích tại sao −3+7=4−3+7=4.
- So sánh 5−(−3)5−(−3) và 5+35+3.
-
Bài tập thực hành
- Tính các phép cộng và trừ sau:
- 12+(−5)12+(−5)
- −9+(−4)−9+(−4)
- 6−(−2)6−(−2)
- −7−8−7−8
- Tính các phép cộng và trừ sau:
-
Bài tập nâng cao
- Tìm giá trị của x sao cho: 𝑥+(−5)=2x+(−5)=2
- Tính tổng của các số nguyên trong khoảng từ -10 đến 10.
Đáp Án:
Phần 1: Cộng Hai Số Nguyên
-
Cộng hai số nguyên cùng dấu
- 5+3=85+3=8
- −4+(−6)=−10−4+(−6)=−10
-
Cộng hai số nguyên khác dấu
- 7+(−2)=57+(−2)=5
- −5+8=3−5+8=3
Phần 2: Tính Chất của Phép Cộng Hai Số Nguyên
-
Tính giao hoán
- Ví dụ: 3+(−5)=−5+33+(−5)=−5+3
-
Tính kết hợp
- Ví dụ: (2+3)+4=2+(3+4)(2+3)+4=2+(3+4)
-
Phần tử 0
- Ví dụ: −7+0=−7−7+0=−7
Phần 3: Phép Trừ Hai Số Nguyên
- Bài tập thực hành
- 8−5=38−5=3
- −3−4=−7−3−4=−7
- 7−(−2)=97−(−2)=9
- −6−(−3)=−3−6−(−3)=−3
Phần 4: Quy Tắc Dấu Ngoặc
- Bài tập thực hành
- −(3+5)=−3−5=−8−(3+5)=−3−5=−8
- −(−7+2)=7−2=5−(−7+2)=7−2=5
- +(4−6)=4−6=−2+(4−6)=4−6=−2
- −(−8−3)=8+3=11−(−8−3)=8+3=11
Kết Luận
- Học sinh nên làm thêm các bài tập tương tự để nắm vững khái niệm và kỹ năng.
- Giáo viên có thể cung cấp thêm bài tập và các hoạt động thực hành để học sinh củng cố kiến thức.
Phép nhân và phép chia hết hai số nguyên - Lớp 6
1. Nhân hai số nguyên khác dấu
- Tích của hai số nguyên khác dấu luôn luôn là số nguyên âm.
- Khi nhân hai số nguyên khác dấu, ta nhân hai số nguyên, rồi thêm dấu trừ (-) vào kết quả.
- Ví dụ: (−3)×4=−12(−3)×4=−12
2. Nhân hai số nguyên cùng dấu
- Tích của hai số nguyên cùng dấu luôn luôn là số nguyên dương.
- Ví dụ: 3×4=123×4=12 và (−3)×(−4)=12(−3)×(−4)=12
3. Tính chất của phép nhân các số nguyên
- Tính giao hoán: 𝑎×𝑏=𝑏×𝑎a×b=b×a
- Ví dụ: 2×3=3×2=62×3=3×2=6
- Tính kết hợp: (𝑎×𝑏)×𝑐=𝑎×(𝑏×𝑐)(a×b)×c=a×(b×c)
- Ví dụ: (2×3)×4=2×(3×4)=24(2×3)×4=2×(3×4)=24
- Tính chất phân phối của phép nhân đối với phép cộng: 𝑎(𝑏+𝑐)=𝑎𝑏+𝑎𝑐a(b+c)=ab+ac
- Ví dụ: 2(3+4)=2×3+2×4=6+8=142(3+4)=2×3+2×4=6+8=14
4. Quan hệ chia hết và phép chia hết trong tập hợp số nguyên
- Trong phép chia hết, dấu của thương của hai số cũng là dấu của tích.
- Ví dụ: 12÷(−4)=−312÷(−4)=−3 và (−12)÷4=−3(−12)÷4=−3
5. Bội và ước của một số nguyên
- Bội: Số nguyên 𝑎a là bội của số nguyên 𝑏b nếu tồn tại một số nguyên 𝑘k sao cho 𝑎=𝑏×𝑘a=b×k.
- Ví dụ: 15 là bội của 3 vì 15=3×515=3×5
- Ước: Số nguyên 𝑏b là ước của số nguyên 𝑎a nếu 𝑎a chia hết cho 𝑏b, tức là tồn tại một số nguyên 𝑘k sao cho 𝑎=𝑏×𝑘a=b×k.
- Ví dụ: 3 là ước của 15 vì 15÷3=515÷3=5
Nhận dạng hình: Hình vuông, Tam giác đều, Lục giác đều
Trong thế giới hình học, các hình dạng cơ bản như hình vuông, tam giác đều và lục giác đều đóng vai trò quan trọng trong việc giúp chúng ta hiểu về các yếu tố cấu thành và tính chất của hình học. Chúng ta sẽ cùng nhau khám phá và tìm hiểu những đặc điểm nổi bật của ba loại hình này.
Hình Vuông là một hình tứ giác đặc biệt với bốn cạnh bằng nhau và bốn góc vuông. Hình vuông có những tính chất đáng chú ý như: các đường chéo của hình vuông bằng nhau và vuông góc với nhau, chia hình vuông thành bốn tam giác vuông bằng nhau. Diện tích của hình vuông được tính bằng cách nhân cạnh với chính nó, và chu vi là tổng của bốn cạnh.
Tam Giác Đều là một hình tam giác có ba cạnh và ba góc bằng nhau. Mỗi góc trong của tam giác đều bằng 60 độ, và các đường cao, đường trung trực, đường trung bình và đường trung tuyến của nó đều trùng nhau. Tam giác đều không chỉ đẹp mắt về mặt hình học mà còn có nhiều ứng dụng trong thực tế, như việc xây dựng các công trình kiến trúc và thiết kế các mẫu hoa văn.
Lục Giác Đều là một hình có sáu cạnh và sáu góc bằng nhau. Mỗi góc trong của lục giác đều bằng 120 độ. Một lục giác đều có thể được tạo thành từ sáu tam giác đều nhỏ hơn, giúp chúng ta dễ dàng tính toán diện tích và chu vi của nó. Lục giác đều thường xuất hiện trong tự nhiên, ví dụ như hình dạng tổ ong, vì nó cho phép tối ưu hóa không gian và vật liệu.
Việc nhận biết và hiểu rõ các yếu tố cơ bản của hình vuông, tam giác đều và lục giác đều không chỉ giúp các em học sinh nắm vững kiến thức hình học cơ bản mà còn phát triển tư duy logic và khả năng giải quyết vấn đề. Thông qua các bài tập và câu hỏi trắc nghiệm, các em sẽ được rèn luyện kỹ năng nhận dạng, mô tả và tạo dựng các hình học này một cách chính xác và hiệu quả.
Hy vọng bài tập này sẽ giúp các em học sinh lớp 6 có cái nhìn tổng quan và sự hứng thú trong việc học tập các hình dạng cơ bản của hình học.
Thông qua bài học này các em đã làm được những gì?
- Nhận dạng hình "Hình vuông, Tam giác đều, Lục giác đều"
- Mô tả được một số yếu tố cơ bản về Hình vuông, Tam giác đều, Lục giác đều
- Tạo được lục giác đều, thông qua các tam giác đều
Nội dung câu hỏi trắc nghiệm nhận dạng hình: Hình vuông, Tam giác đều, Lục giác đều, lớp 6:
1. Hình nào có 4 cạnh bằng nhau và 4 góc vuông?
A. Hình chữ nhật
B. Hình vuông
C. Hình tam giác
D. Hình tròn
2. Hình nào có 3 cạnh bằng nhau và 3 góc bằng nhau?
A. Hình vuông
B. Hình chữ nhật
C. Tam giác đều
D. Lục giác đều
3. Hình nào có 6 cạnh bằng nhau và 6 góc bằng nhau?
A. Tam giác đều
B. Lục giác đều
C. Hình vuông
D. Hình chữ nhật
4. Một hình có 4 góc vuông, đó là hình gì?
A. Tam giác đều
B. Hình vuông
C. Lục giác đều
D. Hình thang
5. Hình nào có tất cả các cạnh và góc đều bằng nhau?
A. Tam giác đều
B. Hình vuông
C. Lục giác đều
D. Cả A, B và C
6. Hình nào có 3 cạnh và 3 góc?
A. Tam giác đều
B. Hình vuông
C. Lục giác đều
D. Hình thoi
7. Hình nào có 6 cạnh?
A. Hình vuông
B. Tam giác đều
C. Lục giác đều
D. Hình bình hành
8. Hình nào có đường chéo bằng nhau và vuông góc?
A. Tam giác đều
B. Hình vuông
C. Lục giác đều
D. Hình chữ nhật
9. Hình nào có tổng các góc bằng 180 độ?
A. Tam giác đều
B. Hình vuông
C. Lục giác đều
D. Hình chữ nhật
10. Hình nào có tổng các góc bằng 720 độ?
A. Tam giác đều
B. Hình vuông
C. Lục giác đều
D. Hình thoi
Mô tả các yếu tố cơ bản của Hình vuông, Tam giác đều, Lục giác đều
11. Hình vuông có mấy đường chéo?
A. 1
B. 2
C. 3
D. 4
12. Góc trong của một tam giác đều bằng bao nhiêu độ?
A. 45
B. 60
C. 90
D. 120
13. Lục giác đều có mấy trục đối xứng?
A. 2
B. 3
C. 4
D. 6
14. Đường chéo của hình vuông chia hình vuông thành mấy phần bằng nhau?
A. 2
B. 3
C. 4
D. 6
15. Diện tích của tam giác đều có cạnh a là:
A. a²/2
B. (a²)/4
C. (a²)/3
D. (a²)/4
16. Chu vi của lục giác đều có cạnh a là:
A. 2a
B. 4a
C. 6a
D. a²
17. Đường chéo lớn của lục giác đều có cạnh a là:
A. 2a
B. 3a
C. 4a
D. 5a
18. Tất cả các góc trong hình vuông đều bằng bao nhiêu độ?
A. 45
B. 60
C. 90
D. 120
19. Tổng số góc trong của lục giác đều là:
A. 360
B. 540
C. 720
D. 900
20. Tam giác đều có mấy đường cao?
A. 1
B. 2
C. 3
D. 4
Hình chữ nhật
- Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
- Tính chất:
- Các cạnh đối song song và bằng nhau.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Góc: Mỗi góc của hình chữ nhật đều bằng 90 độ.
- Công thức diện tích: 𝑆=𝑎×𝑏S=a×b (trong đó 𝑎a và 𝑏b là chiều dài và chiều rộng của hình chữ nhật).
Hình thoi
- Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
- Tính chất:
- Các cạnh đối song song.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Góc: Các góc đối bằng nhau.
- Công thức diện tích: 𝑆=12×𝑑1×𝑑2S=21×d1×d2 (trong đó 𝑑1d1 và 𝑑2d2 là độ dài hai đường chéo).
Hình bình hành
- Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song và bằng nhau.
- Tính chất:
- Các cạnh đối bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Góc: Tổng của hai góc kề nhau bằng 180 độ.
- Công thức diện tích: 𝑆=𝑎×ℎS=a×h (trong đó 𝑎a là cạnh đáy và ℎh là chiều cao).
Hình thang cân
- Định nghĩa: Hình thang cân là hình thang có hai cạnh bên bằng nhau.
- Tính chất:
- Hai cạnh đáy song song.
- Hai cạnh bên bằng nhau.
- Hai góc kề một đáy bằng nhau.
- Góc: Tổng của hai góc kề một đáy bằng 180 độ.
- Công thức diện tích: 𝑆=12×(𝑎+𝑏)×ℎS=21×(a+b)×h (trong đó 𝑎a và 𝑏b là hai cạnh đáy và ℎh là chiều cao).
20 câu hỏi trắc nghiệm toán lớp 6 về Hình chữ nhật, hình thoi, hình bình hành và hình thang cân
Nhận dạng hình và các tính chất cơ bản
1. Hình nào dưới đây có bốn góc vuông?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình thang cân
2. Hình nào dưới đây có bốn cạnh bằng nhau và hai đường chéo vuông góc?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình thang cân
3. Hình nào dưới đây có hai cặp cạnh đối song song và bằng nhau?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Cả ba hình trên
4. Hình nào dưới đây có một cặp cạnh song song và hai cạnh bên bằng nhau?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình thang cân
5. Trong các hình dưới đây, hình nào có đường chéo bằng nhau nhưng không vuông góc?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình thang cân
6. Trong hình thoi, đường chéo chia hình thoi thành:
A. Hai tam giác đều
B. Hai tam giác vuông
C. Hai tam giác cân
D. Hai tam giác tù
Mô tả các yếu tố cơ bản
7. Góc ở hình chữ nhật là bao nhiêu độ?
A. 60 độ
B. 90 độ
C. 120 độ
D. 180 độ
8. Trong hình bình hành, hai đường chéo:
A. Bằng nhau
B. Vuông góc nhau
C. Chia đôi nhau
D. Bằng nhau và vuông góc nhau
9. Hình thang cân có bao nhiêu trục đối xứng?
A. 1
B. 2
C. 3
D. 4
10. Độ dài các cạnh của hình thoi có tính chất gì?
A. Bằng nhau
B. Khác nhau
C. Chỉ có cặp cạnh đối bằng nhau
D. Không xác định
11. Trong hình bình hành, tổng hai góc kề nhau bằng:
A. 90 độ
B. 180 độ
C. 270 độ
D. 360 độ
12. Hình nào dưới đây có hai đường chéo cắt nhau tại trung điểm của mỗi đường?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Cả ba hình trên
13. Trong hình thang cân, hai góc kề một đáy có tính chất gì?
A. Bằng nhau
B. Khác nhau
C. Bằng 90 độ
D. Không xác định
14. Hình chữ nhật có đường chéo dài hơn cạnh nào?
A. Cạnh dài
B. Cạnh ngắn
C. Bằng cạnh dài
D. Bằng cạnh ngắn
15. Trong hình bình hành, tổng các góc trong một tam giác vuông bằng:
A. 90 độ
B. 180 độ
C. 270 độ
D. 360 độ
Nhận dạng và phân biệt hình
16. Hình nào dưới đây vừa là hình thoi vừa là hình bình hành?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình thang cân
17. Đường chéo của hình chữ nhật chia hình thành:
A. Hai tam giác đều
B. Hai tam giác vuông
C. Hai tam giác cân
D. Hai tam giác tù
18. Hình nào dưới đây có diện tích bằng tích của hai cạnh kề?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình thang cân
19. Trong hình thang cân, tổng của hai góc kề một đáy bằng:
A. 90 độ
B. 180 độ
C. 270 độ
D. 360 độ
20. Hình nào dưới đây có tất cả các góc đều bằng 90 độ và các cạnh bằng nhau?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Hình thang cân
Hy vọng rằng những câu hỏi này sẽ giúp học sinh nắm vững kiến thức về hình học và các tính chất của các hình đã học.
Thực hành
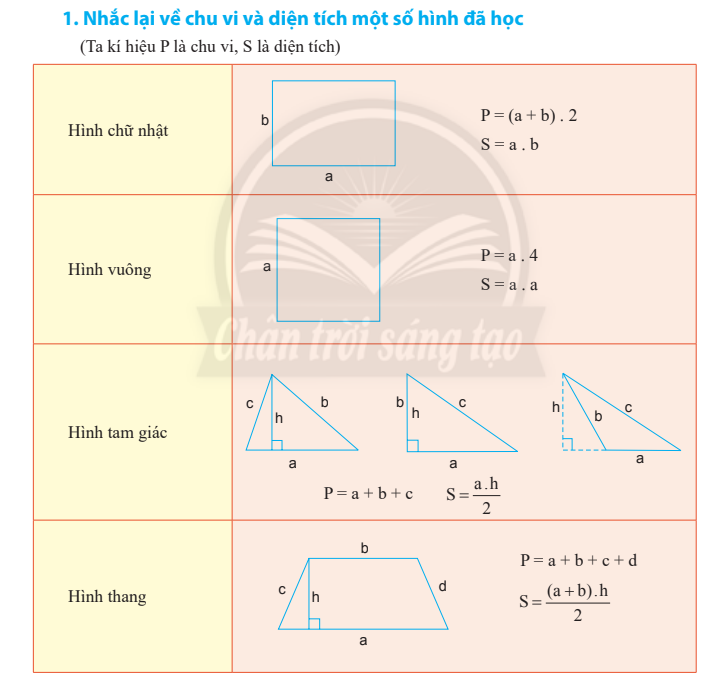
Toán Lớp 6: Tính chu vi và diện tích các hình
Trong chương trình toán lớp 6, việc học cách tính chu vi và diện tích của các hình học cơ bản như hình chữ nhật, hình vuông, hình tam giác, hình thoi, hình bình hành và hình thang cân là rất quan trọng. Các kiến thức này không chỉ giúp học sinh hiểu rõ hơn về các khái niệm hình học mà còn giúp họ áp dụng vào nhiều tình huống thực tế trong cuộc sống hàng ngày.
Mục Tiêu
- Hiểu và nhớ công thức tính chu vi và diện tích của các hình học cơ bản.
- Phát triển kỹ năng tư duy logic và khả năng áp dụng kiến thức vào thực tiễn.
- Nâng cao khả năng giải quyết vấn đề thông qua các bài tập thực tế.
Nội dung bài tập:
Bài tập này bao gồm 20 câu hỏi trắc nghiệm từ dễ đến khó, kèm theo hình vẽ minh họa chi tiết. Các câu hỏi yêu cầu học sinh tính toán chu vi và diện tích của các hình học cơ bản.
Các Chủ Đề Chính
-
Hình Chữ Nhật
- Công thức chu vi: 𝑃=2×(𝑑𝑎ˋ𝑖+𝑟ộ𝑛𝑔)
- Công thức diện tích: 𝑆=𝑑𝑎ˋ𝑖×𝑟ộ𝑛𝑔
-
Hình Vuông
- Công thức chu vi: 𝑃=4×𝑐ạ𝑛ℎ
- Công thức diện tích: 𝑆=𝑐ạ𝑛ℎ×2
-
Hình Tam Giác
- Công thức chu vi: 𝑃=𝑎+𝑏+𝑐
- Công thức diện tích (tam giác vuông): 𝑆=1/2×đ𝑎ˊ𝑦×𝑐ℎ𝑖𝑒^ˋ𝑢𝑐𝑎𝑜
-
Hình Thoi
- Công thức chu vi: 𝑃=4×𝑐ạ𝑛ℎ
- Công thức diện tích: 𝑆=1/2×(đườ𝑛𝑔𝑐ℎ𝑒ˊ𝑜𝑑𝑎ˋ𝑖×đườ𝑛𝑔𝑐ℎ𝑒ˊ𝑜𝑛𝑔𝑎˘ˊ𝑛)
-
Hình Bình Hành
- Công thức chu vi: 𝑃=2×(𝑐ạ𝑛ℎ𝑑𝑎ˋ𝑖+𝑐ạ𝑛ℎ𝑛𝑔𝑎˘ˊ𝑛)
- Công thức diện tích: 𝑆=𝑐ạ𝑛ℎđ𝑎ˊ𝑦×𝑐ℎ𝑖𝑒^ˋ𝑢𝑐𝑎𝑜
-
Hình Thang Cân
- Công thức diện tích: 𝑆=1/2×(đ𝑎ˊ𝑦𝑙ớ𝑛+đ𝑎ˊ𝑦𝑛ℎỏ)×𝑐ℎ𝑖𝑒^ˋ𝑢𝑐𝑎𝑜
Phương Pháp Học Tập
- Vẽ Hình: Học sinh cần vẽ lại hình theo mô tả để có thể dễ dàng hình dung và tính toán.
- Áp Dụng Công Thức: Sử dụng các công thức đã học để tính toán chu vi và diện tích.
- Giải Thích Kết Quả: Đảm bảo hiểu rõ quá trình giải bài để có thể giải quyết các bài toán tương tự trong thực tế.
Bài Tập Trắc Nghiệm
Dưới đây là 20 câu hỏi trắc nghiệm về tính chu vi và diện tích các hình học trong thực tế, từ dễ đến khó.
1. Dễ
-
Hình chữ nhật
- Hình vẽ: Một hình chữ nhật có chiều dài 10cm và chiều rộng 5cm.
- Câu hỏi: Chu vi của hình chữ nhật là bao nhiêu?
- A. 15cm
- B. 30cm
- C. 25cm
- D. 35cm
- Đáp án: B
-
Hình chữ nhật
- Hình vẽ: Một hình chữ nhật có chiều dài 10cm và chiều rộng 5cm.
- Câu hỏi: Diện tích của hình chữ nhật là bao nhiêu?
- A. 50cm²
- B. 30cm²
- C. 25cm²
- D. 15cm²
- Đáp án: A
-
Hình vuông
- Hình vẽ: Một hình vuông có cạnh dài 4cm.
- Câu hỏi: Chu vi của hình vuông là bao nhiêu?
- A. 12cm
- B. 16cm
- C. 20cm
- D. 24cm
- Đáp án: B
-
Hình vuông
- Hình vẽ: Một hình vuông có cạnh dài 4cm.
- Câu hỏi: Diện tích của hình vuông là bao nhiêu?
- A. 12cm²
- B. 16cm²
- C. 20cm²
- D. 24cm²
- Đáp án: B
-
Hình tam giác
- Hình vẽ: Một tam giác có các cạnh lần lượt là 3cm, 4cm và 5cm.
- Câu hỏi: Chu vi của tam giác là bao nhiêu?
- A. 9cm
- B. 10cm
- C. 11cm
- D. 12cm
- Đáp án: D
2. Trung bình
-
Hình thoi
- Hình vẽ: Một hình thoi có các cạnh dài 6cm và hai đường chéo lần lượt là 8cm và 6cm.
- Câu hỏi: Diện tích của hình thoi là bao nhiêu?
- A. 24cm²
- B. 28cm²
- C. 30cm²
- D. 20cm²
- Đáp án: A
-
Hình bình hành
- Hình vẽ: Một hình bình hành có cạnh đáy dài 12cm và chiều cao 8cm.
- Câu hỏi: Diện tích của hình bình hành là bao nhiêu?
- A. 80cm²
- B. 84cm²
- C. 96cm²
- D. 108cm²
- Đáp án: C
-
Hình thang cân
- Hình vẽ: Một hình thang cân có đáy lớn dài 10cm, đáy nhỏ dài 6cm và chiều cao là 4cm.
- Câu hỏi: Diện tích của hình thang là bao nhiêu?
- A. 28cm²
- B. 30cm²
- C. 32cm²
- D. 34cm²
- Đáp án: C
-
Hình chữ nhật
- Hình vẽ: Một hình chữ nhật có chiều dài 15cm và chiều rộng 8cm.
- Câu hỏi: Chu vi của hình chữ nhật là bao nhiêu?
- A. 30cm
- B. 46cm
- C. 54cm
- D. 56cm
- Đáp án: B
-
Hình vuông
- Hình vẽ: Một hình vuông có cạnh dài 7cm.
- Câu hỏi: Diện tích của hình vuông là bao nhiêu?
- A. 49cm²
- B. 56cm²
- C. 63cm²
- D. 70cm²
- Đáp án: A
3. Khó
-
Hình bình hành
- Hình vẽ: Một hình bình hành có cạnh đáy dài 10cm, cạnh bên dài 8cm và góc giữa cạnh đáy và cạnh bên là 60 độ.
- Câu hỏi: Chiều cao của hình bình hành là bao nhiêu?
- A. 6cm
- B. 7cm
- C. 8cm
- D. 9cm
- Đáp án: A
-
Hình thoi
- Hình vẽ: Một hình thoi có cạnh dài 10cm và góc giữa hai cạnh kề là 45 độ.
- Câu hỏi: Diện tích của hình thoi là bao nhiêu?
- A. 50cm²
- B. 70cm²
- C. 100cm²
- D. 120cm²
- Đáp án: C
-
Hình chữ nhật
- Hình vẽ: Một hình chữ nhật có chu vi là 40cm và chiều dài là 12cm.
- Câu hỏi: Chiều rộng của hình chữ nhật là bao nhiêu?
- A. 8cm
- B. 7cm
- C. 6cm
- D. 5cm
- Đáp án: C
-
Hình thang cân
- Hình vẽ: Một hình thang cân có đáy lớn dài 14cm, đáy nhỏ dài 6cm và chiều cao là 5cm.
- Câu hỏi: Diện tích của hình thang là bao nhiêu?
- A. 50cm²
- B. 40cm²
- C. 60cm²
- D. 70cm²
- Đáp án: A
-
Hình bình hành
- Hình vẽ: Một hình bình hành có diện tích là 84cm² và cạnh đáy dài 14cm.
- Câu hỏi: Chiều cao của hình bình hành là bao nhiêu?
- A. 5cm
- B. 6cm
- C. 7cm
- D. 8cm
- Đáp án: C
-
Hình thoi
- Hình vẽ: Một hình thoi có chu vi là 40cm. Độ dài của một cạnh là bao nhiêu?
- A. 5cm
- B. 8cm
- C. 10cm
- D. 12cm
- Đáp án: C
- Hình vẽ: Một hình thoi có chu vi là 40cm. Độ dài của một cạnh là bao nhiêu?
-
Hình thang
- Hình vẽ: Một hình thang có đáy lớn dài 18m, đáy nhỏ dài 12m và chiều cao là 10m.
- Câu hỏi: Diện tích của hình thang là bao nhiêu?
- A. 150m²
- B. 180m²
- C. 200m²
- D. 220m²
- Đáp án: C
-
Hình tam giác vuông
- Hình vẽ: Một tam giác vuông có cạnh góc vuông là 6cm và 8cm.
- Câu hỏi: Độ dài cạnh huyền của tam giác là bao nhiêu?
- A. 8cm
- B. 9cm
- C. 10cm
- D. 11cm
- Đáp án: C
-
Hình tam giác đều
- Hình vẽ: Một tam giác đều có cạnh dài 6cm.
- Câu hỏi: Chu vi của tam giác đều là bao nhiêu?
- A. 12cm
- B. 18cm
- C. 24cm
- D. 30cm
- Đáp án: B
-
Hình chữ nhật
- Hình vẽ: Một hình chữ nhật có chiều dài 10cm và chiều rộng 5cm, trên hình có một đường chéo nối từ một góc tới góc đối diện.
- Câu hỏi: Độ dài của đường chéo là bao nhiêu?
- A. 10cm
- B. 11cm
- C. 12cm
- D. 13cm
- Đáp án: C
Kết Luận
Bài tập "Tính Chu Vi và Diện Tích Các Hình Trong Thực Tế" không chỉ giúp học sinh nắm vững kiến thức hình học mà còn rèn luyện khả năng tư duy logic
Các bài toán tính chu vi, diện tích trong thực tế cho lớp 6
Mục tiêu bài học
Bài học này nhằm giới thiệu cho học sinh lớp 6 về các bài toán tính chu vi và diện tích các hình dạng trong thực tế. Học sinh sẽ học cách áp dụng các công thức toán học vào các tình huống thực tế và phát triển kỹ năng giải quyết vấn đề.
Khái niệm cơ bản
- Chu vi: Chu vi của một hình là tổng độ dài của tất cả các cạnh của hình đó. Ví dụ, chu vi của một hình chữ nhật là tổng của hai lần chiều dài và hai lần chiều rộng.
- Diện tích: Diện tích của một hình là không gian bên trong hình đó. Ví dụ, diện tích của một hình chữ nhật là tích của chiều dài và chiều rộng.
Các hình dạng phổ biến
- Hình chữ nhật:
- Chu vi: 𝑃=2(𝑙+𝑤)P=2(l+w)
- Diện tích: 𝐴=𝑙×𝑤A=l×w
- Hình vuông:
- Chu vi: 𝑃=4×𝑠P=4×s
- Diện tích: 𝐴=𝑠2A=s2
- Hình tam giác:
- Chu vi: 𝑃=𝑎+𝑏+𝑐P=a+b+c
- Diện tích: 𝐴=12×𝑏×ℎA=21×b×h
- Hình tròn:
- Chu vi: 𝑃=2𝜋𝑟P=2πr
- Diện tích: 𝐴=𝜋𝑟2A=πr2
Ứng dụng trong thực tế
- Thiết kế sân vườn: Học sinh có thể tính chu vi và diện tích của các khu vực trong sân vườn để biết cần bao nhiêu vật liệu để xây hàng rào hoặc trải cỏ.
- Trang trí nội thất: Tính diện tích các bức tường để sơn hoặc dán giấy tường.
- Xây dựng: Tính toán chu vi và diện tích để xác định số lượng vật liệu cần thiết cho việc xây dựng nền móng, sàn nhà hoặc mái nhà.
Bài tập thực hành:
1. Trong bãi giữ xe người ta đang vẽ một mủi tên với kích thước như hình, để hướng dẫn xe chạy, tính diện tích mủi tên?
-
A. 1.8m2
-
B. 2.2m2
-
C. 2.4m2
-
D. 36 m2
2. Trong một khu vườn hình chữ nhật, người ta làm một lối đi lát sỏi, với kích thước như hình vẽ, chi phí cho mỗi m2(vuông) làm lối đi là 120 nghìn đồng. Hỏi chi phí làm lối đi là bao nhiêu?
-
A. 4 nghìn
-
B. 4.800 nghìn
-
C. 5 nghìn
-
D. 5.400 nghìn
3. Người ta cần xây tường rào cho một khu vườn như hình bên, mỗi mét tới tốn 150 nghìn. Hỏi cần bao nhiêu tiền để xây tường rào?
-
A. 4 triệu
-
B. 5.800 nghìn
-
C. 6.600 nghìn
-
D. 7.200 nghìn
4. Tính diện tích hình sau?
-
A. 43 cm2
-
B. 45 cm2
-
C. 49 cm2
-
D. 50 cm2
5. Tính chu vi hình sau?
-
A. 43m
-
B. 45m
-
C. 49m
-
D. 56m
6. Tính diện tính hình được tô màu sau:
-
A. 129m2
-
B. 153m2
-
C. 48m2
-
D. 105m2
7. Một mảnh vườn có hình dạng như hình vẽ bên. Để tính diện tích mảnh vườn, người ta chia nó thành hình thang cân ABCD và hình bình hành ADEF có kích thước như sau: BC = 30m; AD= 42m; BM= 22m; EN= 28m. Hãy tính diện tích mảnh vườn này?
-
A. 1900 m2
-
B. 1968 m2
-
C. 2320 m2
-
D. 4867 m2
8. Một khu vườn hình chữ nhật có chiều dài 25m, chiều rộng 15m, ở giữa khu vườn người ta xây một bồn hoa có độ dài 2 đường chéo lần lược là 5m và 3m. Tính diện tích phần còn lại của khu vườn:
-
A. 4000 m2
-
B. 255.5 m2
-
C. 1730 m2
-
D. 367.5 m2
Kết luận
Việc tính toán chu vi và diện tích không chỉ là kiến thức toán học cơ bản mà còn có ứng dụng rộng rãi trong cuộc sống hàng ngày. Hiểu và áp dụng đúng các công thức này giúp học sinh phát triển khả năng tư duy logic và giải quyết vấn đề thực tế một cách hiệu quả.
Bài tập "Thu thập và phân loại" Toán lớp 6 Online
Chủ đề: Thống kê số lần gõ bàn phím máy tính của các từ
Mục tiêu
- Học sinh biết cách thu thập và thống kê dữ liệu số lần gõ bàn phím của các từ.
- Học sinh biết cách phân loại và trình bày dữ liệu.
- Học sinh phát triển kỹ năng sử dụng công cụ trực tuyến để thu thập và phân tích dữ liệu.
Hướng dẫn thực hiện
Bài tập 1: Thu thập dữ liệu
- Mỗi học sinh sẽ sử dụng một phần mềm đếm số lần gõ phím này
- Thực hiện đếm số lần gõ bàn phím của các từ sau:
- Go to school
- Classroom
- Sunny
- Eat breakfast
- Living room
- WindowOut Door
- RoofBrush teeth
- Take a shower
- Read bookSwimming
- RunningBasketball
- FootballDo homework
- RabbitTiger Beer
- Elephant
- Snow white
Bài tập 2: Ghi chép và phân loại dữ liệu
- Ghi lại số lần gõ phím của mỗi từ vào bảng thống kê như sau:
| Từ | Số lần gõ phím |
|---|---|
| G | |
| T | |
| S | |
| O | |
| L | |
| ... | ... |
- Mỗi học sinh sẽ thực hiện bài tập này ít nhất 3 lần với các từ xuất hiện ngẫu nhiên như trên, kết hợp với học tiếng anh
- Rồi ghi kết quả vào các ô phía dưới
Bài tập 3: Tính toán và trình bày dữ liệu
- Tính toán tổng số lần gõ phím của chữ cái, khi xuất hiện 1 từ
- Tính số trung bình cộng của số lần gõ phím cho mỗi từ.
Bài tập 4: Trình bày dữ liệu
- Sử dụng bảng tính (ví dụ: Microsoft Excel, Google Sheets) để nhập và tính toán dữ liệu.
- Trình bày dữ liệu dưới dạng biểu đồ cột hoặc biểu đồ tròn để so sánh số lần gõ phím của các từ.
Bài tập 5: Thảo luận và rút ra kết luận
- Học sinh thảo luận về kết quả thu thập và phân loại dữ liệu trong một buổi học trực tuyến.
- Trả lời các câu hỏi thảo luận:
- Từ nào có số lần gõ phím nhiều nhất? Tại sao?
- Từ nào có số lần gõ phím ít nhất? Tại sao?
- Làm thế nào để cải thiện kỹ năng thu thập và phân loại dữ liệu trực tuyến?
Yêu cầu nộp bài
- Mỗi học sinh nộp báo cáo bằng văn bản hoặc bản điện tử về quá trình và kết quả thu thập, phân loại dữ liệu.
- Đính kèm các bảng thống kê và biểu đồ liên quan.
- Gửi bài qua email hoặc hệ thống học tập trực tuyến của lớp.
- Giáo viên kiểm tra kết quả học sinh tại website trên
Mục tiêu: Bài học "Biểu diễn dữ liệu trên bảng" giúp học sinh hiểu và thực hành các kỹ năng cơ bản trong việc thu thập, tổ chức và trình bày dữ liệu dưới dạng bảng. Đây là một kỹ năng quan trọng không chỉ trong toán học mà còn trong nhiều lĩnh vực khác của đời sống và học tập.
Nội dung chính:
-
Khái niệm về Dữ liệu và Bảng:
- Giới thiệu khái niệm dữ liệu và cách thu thập dữ liệu.
- Giải thích bảng là một công cụ để tổ chức và trình bày dữ liệu một cách rõ ràng và có hệ thống.
-
Các Thành Phần của Bảng:
- Hàng và cột.
- Tiêu đề của bảng và tiêu đề của các cột.
- Các ô dữ liệu.
-
Cách Lập Bảng:
- Bước 1: Xác định dữ liệu cần thu thập.
- Bước 2: Thiết kế bảng với các tiêu đề phù hợp.
- Bước 3: Điền dữ liệu vào bảng một cách chính xác.
-
Phân Tích và Diễn Giải Dữ Liệu Từ Bảng:
- Cách đọc và hiểu thông tin từ bảng.
- Phân tích các xu hướng và so sánh dữ liệu.
Hoạt động học tập:
- Hoạt động nhóm: Học sinh sẽ được chia thành các nhóm nhỏ để thu thập dữ liệu từ một chủ đề cụ thể (ví dụ: số lượng sách trong thư viện, số giờ học của các môn, chiều cao của học sinh trong lớp,...). Mỗi nhóm sẽ lập bảng và trình bày dữ liệu của mình.
- Thảo luận lớp: Mỗi nhóm sẽ trình bày bảng dữ liệu của mình và giải thích cách họ thu thập và tổ chức dữ liệu.
- Bài tập thực hành: Học sinh sẽ làm các bài tập lập bảng và phân tích dữ liệu được giáo viên cung cấp.
Kết luận:
- Học sinh sẽ hiểu rõ tầm quan trọng của việc tổ chức dữ liệu và cách sử dụng bảng để trình bày dữ liệu một cách hiệu quả.
- Kỹ năng lập bảng không chỉ hữu ích trong toán học mà còn trong nhiều môn học và tình huống thực tế khác.
Đánh giá:
- Học sinh sẽ được đánh giá dựa trên khả năng thu thập dữ liệu, lập bảng và phân tích dữ liệu.
- Sự tham gia tích cực trong các hoạt động nhóm và thảo luận lớp cũng sẽ được xem xét trong quá trình đánh giá.
Qua bài học này, học sinh sẽ nắm vững kỹ năng biểu diễn dữ liệu trên bảng, góp phần nâng cao khả năng tư duy logic và tổ chức thông tin của các em.
Bài Học: Hai Phân Số Bằng Nhau
Mục tiêu:
- Hiểu được khái niệm hai phân số bằng nhau.
- Biết cách kiểm tra và chứng minh hai phân số bằng nhau.
Nội dung chính:
-
Khái niệm:
- Hai phân số ( \frac{a}{b} ) và ( \frac{c}{d} ) được gọi là bằng nhau nếu và chỉ khi ( a \times d = b \times c ) với ( b \neq 0 ) và ( d \neq 0 ).
- Điều này có nghĩa là tích của tử số của phân số đầu tiên với mẫu số của phân số thứ hai bằng tích của mẫu số của phân số đầu tiên với tử số của phân số thứ hai.
-
Ví dụ minh họa:
- Ví dụ 1: Xét hai phân số ( \frac{2}{3} ) và ( \frac{4}{6} ).
- Tính ( 2 \times 6 = 12 ).
- Tính ( 3 \times 4 = 12 ).
- Vì ( 12 = 12 ), nên hai phân số này bằng nhau.
- Ví dụ 2: Xét hai phân số ( \frac{3}{4} ) và ( \frac{6}{8} ).
- Tính ( 3 \times 8 = 24 ).
- Tính ( 4 \times 6 = 24 ).
- Vì ( 24 = 24 ), nên hai phân số này bằng nhau.
- Ví dụ 1: Xét hai phân số ( \frac{2}{3} ) và ( \frac{4}{6} ).
-
Quy tắc:
- Để kiểm tra hai phân số có bằng nhau không, có thể theo các bước sau:
- Nhân tử số của phân số thứ nhất với mẫu số của phân số thứ hai.
- Nhân mẫu số của phân số thứ nhất với tử số của phân số thứ hai.
- So sánh hai kết quả. Nếu chúng bằng nhau, hai phân số bằng nhau.
- Để kiểm tra hai phân số có bằng nhau không, có thể theo các bước sau:
-
Luyện tập:
- Bài tập 1: Kiểm tra xem hai phân số ( \frac{5}{7} ) và ( \frac{10}{14} ) có bằng nhau không.
- Bài tập 2: Tìm một phân số bằng với phân số ( \frac{2}{5} ) bằng cách nhân cả tử và mẫu với một số nguyên dương.
Ghi nhớ:
- Hai phân số chỉ bằng nhau khi tỷ lệ giữa tử số và mẫu số của chúng giống nhau sau khi được nhân chéo và so sánh.
- Việc hiểu và xác định phân số bằng nhau giúp thực hiện các phép toán với phân số một cách chính xác.
Hỗn số là gì?
Hỗn số là một dạng số được biểu diễn bởi sự kết hợp của hai thành phần: một số nguyên và một phân số dương có tử số nhỏ hơn mẫu số. Hỗn số thường được sử dụng để biểu diễn các giá trị lớn hơn 1 nhưng không phải là số nguyên hoàn toàn, chẳng hạn như 2 ⅓ (hai và một phần ba). Đây là một cách biểu diễn gọn gàng và dễ hiểu của các phân số lớn hơn 1.
Ví dụ:
- Hỗn số 2132 \dfrac{1}{3}231 có phần số nguyên là 2 và phần phân số là 13\dfrac{1}{3}31.
Phân Tích Phân Số Thành Hỗn Số
Khi làm việc với phân số có tử số lớn hơn mẫu số (phân số lớn hơn 1), chúng ta có thể phân tích chúng thành hỗn số để dễ dàng làm việc và hiểu rõ hơn về giá trị của chúng. Cách làm này giúp tách rời phần nguyên và phần phân số.
Các bước để phân tích phân số thành hỗn số:
-
Chia lấy phần nguyên: Chia tử số cho mẫu số và lấy phần nguyên của phép chia. Đây chính là phần nguyên của hỗn số.
Ví dụ: Với phân số 73\dfrac{7}{3}37, khi chia 7 cho 3, ta được phần nguyên là 2.
-
Tìm phần phân số còn lại: Sau khi lấy phần nguyên, ta tìm phần dư của phép chia. Phần dư này sẽ tạo thành tử số của phần phân số, còn mẫu số giữ nguyên như ban đầu.
Với ví dụ trên, phần dư của phép chia 7÷37 \div 37÷3 là 1. Vậy phần phân số là 13\dfrac{1}{3}31.
-
Viết hỗn số: Kết hợp phần nguyên và phần phân số để tạo thành hỗn số.
Ví dụ: 73\dfrac{7}{3}37 được phân tích thành hỗn số là 2132 \dfrac{1}{3}231.
Kết luận:
Phân tích một phân số thành hỗn số là một phương pháp hữu ích để hiểu rõ giá trị của các phân số lớn hơn 1. Thay vì chỉ làm việc với các phân số phức tạp, việc biểu diễn chúng dưới dạng hỗn số giúp dễ dàng hơn trong việc giải thích và tính toán.